Basics
Graph is a generic structure designed to support relationships. and is defined as a set of vertices $1, 2, .. n$ often labeled and edges usually written as $(vertex_1, vertex_2)$
$E$ is set of edges and $V$ is set of nodes. 2 vertices are adjacent if there is an edge a between those 2 vertices.
Normally we denote $|V| = n$ and $|E| = m$ where $|V|$ is cardinality (number of elements) of a set.
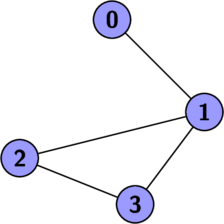
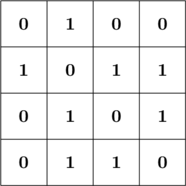
Representation
$E$ is set of edges and $V$ is set of nodes. 2 vertices are adjacent if there is an edge a between those 2 vertices. of a set.
List of all edges i.e $(1, 2), (3, 4), ...$ but its not very convenient to work with.
The second way to represent the graph is the adjacent matrix. Its the simplest way to represent the matrix. Its an $n \times n$ matrix where $e_{ij} = 1$ iff there exist an edge between $i$ and $j$.
There is an important observation in this matrix that diagonal elements are 0 which means there is no edge from a node to itself i.e self loop.
Another common and important way to represent a graph is called an Adjacency List. For each vertix we write down list of vertices that are incident on that vertix.
C++: Implementation
Initializing the structures for un-weighted case.
#include<vector> //We use stl:vector to make lists. #include <utility> using namespace std; int n, m; // number of nodes and edges const int MAXN = 1e5 + 5; // maximum number of vertices possible //Initializing the structures vector<int> G[MAXN]; // an array of vectors (lists) vector< pair< int, int > > E; // list of pair of values bool adj[MAXN][MAXN]; // a matrix of MAXN x MAXN initialized to 0
Initializing the structures for weighted case.
#include<vector> #include <utility> #define ll long long using namespace std; int n, m; // number of nodes and edges const int MAXN = 1e5 + 5; // maximum number of vertices possible //Initializing the structures vector<pair< int, ll > > G[MAXN]; // an array of vectors (lists) vector< pair < pair< int, int >, ll> > E; // list of pair of values ll adj[MAXN][MAXN]; // a matrix of MAXN x MAXN initialized to 0
Inserting edges to the structures for weighted and un-directed case.
for(int i = 0; i < m; i++){ int u, v;ll w; scanf("%d %d %lld", &u, &v, &w); u--; v--; // if starting label of the input is 1 decrease it to make it 0. G[u].push_back({v, w}); G[v].push_back({u, w}); adj[u][v] = w; adj[v][u] = w; E.push_back({{u, v}, w}); }
What is a Cycle ?
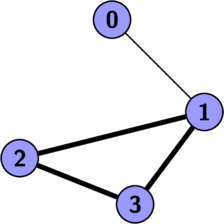
A cycle is a sequence of vertices $v_1, v_2, v_3, ... v_k$ where each $(v_i, v_{i+1})$ is adjacent and $v_1$ is adjacent to $v_k$.
A cycle is simple if all vertices on it are distinct.
What is a Path ? Path Search Problem
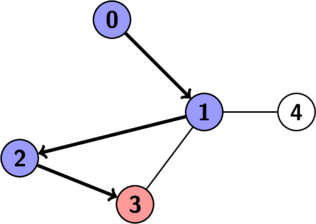
A path is a sequence of vertices $v_1, v_2, v_3, ... v_k$ where each $(v_i, v_{i+1})$ is adjacent.
A path is simple if all vertices are distinct.
Given a graph $G$ and 2 vertices $s$ and $t$. Check if a path from $s$ to $t$ exists ? If it exists print the path.
Think about it as exploring a labyrinth (maze).
What is connectivity ?
Two nodes are connected if there exist a path between them. If I can go from one node to another using the edges of the graph.
Connected components is a set of vertices where each of 2 vertices are connected and no other vertice outside the component is connected .
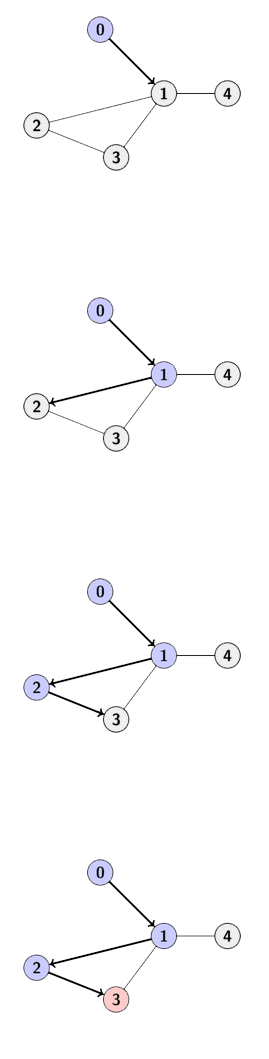
Algorithms: DFS (Depth First Search)
Now lets try to find all the vertices that are connected to some vertice 1.
For ex: Imagine you are trapped in some labyrinth and you want to find out the exit door. You are in some room and don't know where the exit is.
You try first door out of that room. You go to next room and try the first door out of that room. If once you come to a room you already been to you wont enter that room and go back. You try the second door out of the old room and traverse the labyrinth.
There are two types of basic traverses DFS and BFS. They both differ in the order of vertices visited but both of the searches traverses the graph.
In DFS we go through the first door of the first room and then again go through the first door of he second room and similarly we go deeper and deeper till we finally encounter the place we already been. Lets try to formalize it.
Black colored directed edges forms a path tree / DFS tree
Pseudo Code:
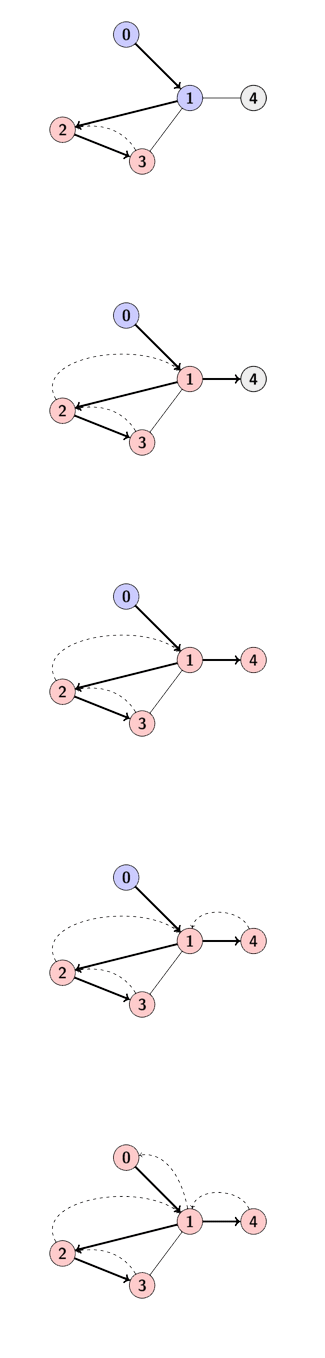
recursive pseudo code visit(_fro): mark _fro visited for all _to adjacent to _fro: if _to is not visited: visit(_to) iterative pseudo code visit(src): initialize stack with src stack := {src} while stack is not empty: _fro := stack.pop() if _fro is not visited: mark _fro visited for all _to adjacent to _fro: push _to to stack
C++ Implementation
recursive definition bool vis[MAXN]; for(int i = 0; i < n; i++) vis[i] = false; for(int i = 0; i < n; i++) if(!vis[i]) dfs(i); void dfs(int fro){ vis[fro] = true; for(int to: G[fro]){ if(vis[to]) continue; dfs(to); } } iterative approach bool vis[MAXN]; for(int i = 0; i < n; i++) vis[i] = false; for(int i = 0; i < n; i++) if(!vis[i]) dfs(i); void dfs(int src){ vector<int> stack; stack.push_back(src); while( !stack.empty() ){ int fro = stack.pop_back(); if(vis[fro]) continue; vis[fro] = true; for(int to: G[fro]) stack.push_back(to); } }
What is the complexity of this algorithm ?

It depends upon how we represent the graph. If we store thegraph as a adjacency matrix its $O(n^2)$. If its stored in adjacency list its $O(n+m)$. Why?
We visit each vertix only once because the in recursive procedure dfs is only called for vertices which is not yet visited and when its called vis[] of the vertice is set true and for each vertice the visit mark is set true only once.
If we store the graph in the adjacency matrix , we have to traverse through all the matrix and find the vertices that are adjacent tofro. For each vertice it takes $O(n)$ to find its adjacent vertices and in total $O(n^2)$ for all vertices.
If we store the graph in adjacency list its $O(n+m)$, and for eachvertice, we can find the adjacent vertice in $O(1)$. and for eachvertice we can touch each adjacent node from it exactly once.and for each vertice we can use each edge going from it exactly once. So if all vertices and edges are touched once so its $O(n+m)$.
Pseudo Code: DFS with colors and time
Properties of Times
For any u and v time segments [tin[u], tout[u]] and [tin[v], tout[v]].
if[tin[u], tout[u]]is nested in[tin[v], tout[v]]means thatuis a de-scendant ofvandvis a ancestor ofuin the DFS / PATH tree.
if[tin[u], tout[u]]and[tin[v], tout[v]]do not intersect - meaning uand v are not comparable.
Type Of Edges:
These classifications are often used for problems like finding bridges and finding articulation points.
Tree Edges : Edges going from GRAY to WHITE vertex in the DFS tree.
Backward Edges : Edges going from GRAY to GRAY vertex in the DFS tree.
Forward Edges (ONLY IN DIRECTED GRAPH) : Edges goingfrom GRAY to BLACK vertex in the DFS tree. If v is a descen-dant of u, then edge (u,v) is a forward edge. In other words, ifwe already visited and exited v and entry[u] entry[v] then theedge (u,v) forms a forward edge.
Cross Edges (ONLY IN DIRECTED GRAPH): Edges goingfrom GRAY to BLACK vertex in the DFS tree. if v is nei-ther an ancestor or descendant of u, then edge (u,v) is a crossedge. In other words, if we already visited and exited v and entry[u] entry[v] then (u,v) is a cross edge.
Look on the times tin / tout to choose forward or cross.
Cycle Detection: Application of DFS
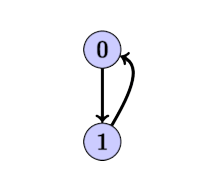
Cycle exists if and only if a backward edge exists, i.e look up from the vertex to a GRAY vertex (careful with un-directed graph skip the edge from which you came to the current)
Why can’t we go from go from a current vertex to a black vertex? Because when we mark the vertex a as black we processed all its edges that out go this vertex and we should have processed all adjacent vertex B that’s the reason we can’t reach a black vertex from the current node and whenever we find a cycle its always an edge from current node to a gray node.
Make sure you distinguish between a cycle and going back to the parent. A separate par in the dfs definition i.e visit(fro, par) because you need to remember where you came from.
Path Tree
Path Tree is an outgoing tree routed at s. Path tree covers all vertices reachable from s.
parent[u] = u for root vertex u = src
parent[u] = −1 for unreachable vertices u
parent[u] = v if v is the previous vertex for u on the path from from s to u.
pseudo code to restore path
Beware of the identifier prev as there exist a std:prev predefined in C++. If you code in other languages then just don’t care.
function pathTo(t):
path := []
while parent[t] != t: //t is not root
push t to path structure
t := parent[t] // go towards root
push t to path // t is root
reverse(path)
return path
Directed case
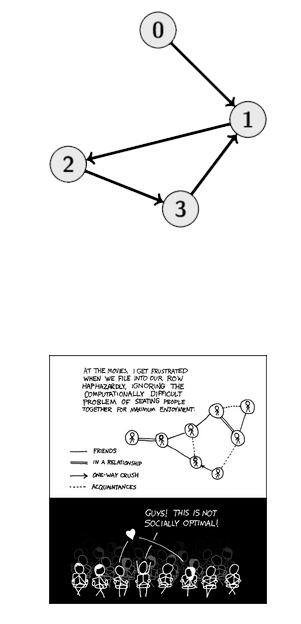
Adjacency matrix is not symmetric in this case.
There can be directed relationships, like if person A can be a friend of person B but not true the other way around.
There can be similar problems like if $u$ is reachable from vertex $v$.
We can extract connected components from the directed graph. They are called Strongly connected components.
Let's try finding a cycle in a directed case. From 1 to 2 and 2 to 3 marks 3 visited and 2 visited and goes 1 to 3 and finds 3 visited and says its a cycle. but there was'nt.
Lets try explicitly state colors with 3 values. 0 means WHITE not yet visited, 1 means gray means visited but not processed, 2 means BLACK means visited an processed.
A cycle only exists only if we go from current node to a gray node.
Shortest Path Problem: Directed or un-directed graph
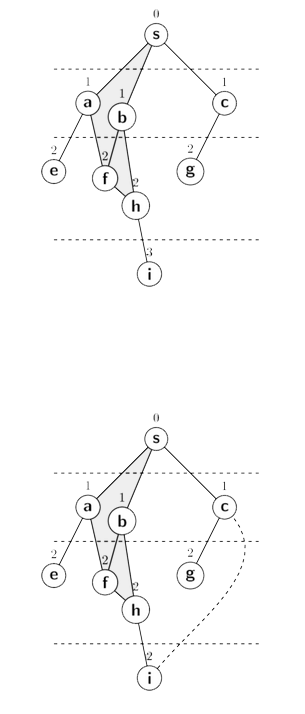
Given a graph G find the shortest path between a pair of vertices $s$ and $t$.
All the edges in my graph is same length.
Lets discuss a simpler but an inefficient algorithm to solve this problem called Flood Fill
We say the best distance from s to s is 0.
Next step is that we consider all adjacent vertices of $s$. and decide that the distance to them is 1. This is so called the first layer.
Now I want to enumerate all those vertices with distance 1 and assign them distance one more than my current distance. There might be some problem that some vertices at level 2 might be adjacent to several vertices from the level 1. TO keep things simple I will just need to assign those vertices which are yet unassigned.
Eventually this way we will cover all the vertices of the connected component that has the vertex $s$.
There are efficient algorithms that does exactly the same thing but a bit faster.
When we have several layers to the bottom and we meet some vertex with length 3 and is connected to some vertex length 1. we would like to assign length 4 to it but this situation will never happen. Why ?
Since we are enumerating vertices in increasing order of the layers, so the vertex with length 3 would actually have assigned a length of 2 since it was connected with a vertex of length 1.
Optimization by Queue
Lets understand how to find those levels efficiently. We will use a data structure called a queue. Queue uses FIFO strategy, which is first in and first out. It behaves like a normal queue in front of a ticket booth.
I have to maintain the queue with initial entry $s$ and I have to maintain a distances[] array to store the distance from $s$. Assume all vertices except $s$ has a very big distance $10^9 + 7$ and s having distance 0.
First thing to do is, to extract a vertex from the queue and we process it. what do we do in processing? To process the vertex I look through all the outgoing edges of this vertex and I try to relax the big distance( $10^9 + 7$) from s to its neighbours to something smaller.
In our case from $s$ we can go to $a$ , $b$ , $c$ in 1 step, so I update their distance to 1 and push all the updated vertices to the queue. Now the vertex $s$ is processed.
The next step is to extract the next vertex from the queue and repeat the same procedure and try to relax (make smaller ) those distances which are larger than current + 1.
Eventually all the vertices in the connected component is assigned.
What is the proof of correctness ?
Why does it works ?
There are 2 observations.
All vertices will eventually in the queue
All vertices will be in the queue exactly once
There cannot be a situation where we relax a vertex and put it in the queue and relax it twice and put it in the queue again.
Lets say a vertex $x$ whose has an edge to a vertex $v$ which has some distance $5$ and $x$ has distance $6$ and there also exist a vertex $u$ which already has a distance say $3$ and also want to relax (make better) distance for $x$ and relax it to 4.
Why cannot this situation happen ?
Because $u$ will be processed first than $v$ as we are processing in increasing order of levels/ layers/ distances. That proves the correctness